Complex Numbers

Introduction. Let us hark back to the first grade when the only numbers you knew were the
ordinary everyday integers. You had no trouble solving problems in which you were, for instance,
asked to find a number x such that 3x = 6. You were quick to answer ”2”. Then, in the second
grade, Miss Holt asked you to find a number x such that 3x = 8. You were stumped—there was
no such ”number”! You perhaps explained to Miss Holt that 3(2) = 6 and 3(3) = 9, and since 8 is
between 6 and 9, you would somehow need a number between 2 and 3, but there isn’t any such
number. Thus were you introduced to ”fractions.”

These fractions, or rational numbers, were defined by Miss Holt to be ordered pairs of
integers—thus, for instance, (8, 3) is a rational number. Two rational numbers (n,m) and (p, q)
were defined to be equal whenever nq = pm. (More precisely, in other words, a rational number is
an equivalence class of ordered pairs, etc.) Recall that the arithmetic of these pairs was then
introduced: the sum of (n,m) and (p,q) was defined by

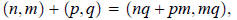
and the product by

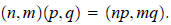
Subtraction and division were defined, as usual, simply as the inverses of the two operations

In the second grade, you probably felt at first like you had thrown away the familiar integers and
were starting over. But no. You noticed that (n, 1) + (p, 1) = (n + p, 1) and also
(n, 1)(p,1) = (np, 1). Thus the set of all rational numbers whose second coordinate is one behave
just like the integers. If we simply abbreviate the rational number (n, 1) by n, there is absolutely no
danger of confusion: 2 + 3 = 5 stands for (2, 1) + (3, 1) = (5, 1). The equation 3x = 8 that started
this all may then be interpreted as shorthand for the equation (3, 1)(u, v) = (8, 1), and one easily
verifies that x = (u, v) = (8, 3) is a solution. Now, if someone runs at you in the night and hands
you a note with 5 written on it, you do not know whether this is simply the integer 5 or whether it is
shorthand for the rational number (5, 1). What we see is that it really doesn’t matter. What we
have ”really” done is expanded the collection of integers to the collection of rational numbers. In
other words, we can think of the set of all rational numbers as including the integers–they are
simply the rationals with second coordinate 1.

One last observation about rational numbers. It is, as everyone must know, traditional to write the
ordered pair (n,m) as n/m. Thus n stands simply for the rational number n/1, etc.

Now why have we spent this time on something everyone learned in the second grade? Because
this is almost a paradigm for what we do in constructing or defining the so-called complex
numbers. Watch.

Euclid showed us there is no rational solution to the equation x^2 = 2. We were thus led to defining
even more new numbers, the so-called real numbers, which, of course, include the rationals. This is
hard, and you likely did not see it done in elementary school, but we shall assume you know all
about it and move along to the equation x^2 = -1. Now we define complex numbers. These are
simply ordered pairs (x, y) of real numbers, just as the rationals are ordered pairs of integers. Two
complex numbers are equal only when there are actually the same–that is (x, y) = (u. v) precisely
when x = u and y = v. We define the sum and product of two complex numbers:

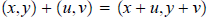
and

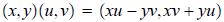
As always, subtraction and division are the inverses of these operations

Now let’s consider the arithmetic of the complex numbers with second coordinate 0:

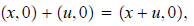
and

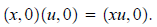
Note that what happens is completely analogous to what happens with rationals with second
coordinate 1. We simply use x as an abbreviation for (x, 0) and there is no danger of confusion:
x + u is short-hand for (x, 0) + (u, 0) = (x + u, 0) and xu is short-hand for (x, 0)(u, 0). We see that
our new complex numbers include a copy of the real numbers, just as the rational numbers include
a copy of the integers.

Next, notice that x(u, v) = (u, v)x = (x, 0)(u, v) = (xu, xv). Now then, any complex number
z = (x, y) may be written

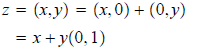
When we let α = (0, 1), then we have

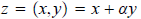
Now, suppose z = (x, y) = x + αy and w = (u, v) = u + αv. Then we have

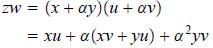
We need only see what α^2 is: α^2 = (0, 1)(0, 1) = (-1, 0), and we have agreed that we can safely
abbreviate (-1, 0) as -1. Thus, α^2 = -1, and so

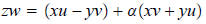
and we have reduced the fairly complicated definition of complex arithmetic simply to ordinary real
arithmetic together with the fact that α^2 = -1.

Let’s take a look at division–the inverse of multiplication. Thus z/w stands for that complex number
you must multiply w by in order to get z . An example:

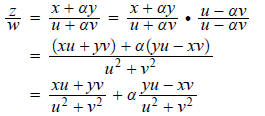
Note this is just fine except when u^2 + v^2 = 0; that is, when u = v = 0. We may thus divide by any
complex number except 0 = (0, 0).

One final note in all this. Almost everyone in the world except an electrical engineer uses the letter
i to denote the complex number we have called α. We shall accordingly use i rather that α to stand
for the number (0, 1).

Exercises

1. Find the following complex numbers in the form x + iy:

2. Find all complex z = (x, y) such that

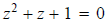
3. Prove that if wz = 0, then w = 0 or z = 0.

Geometry. We now have this collection of all ordered pairs of real numbers, and so there is an
uncontrollable urge to plot them on the usual coordinate axes. We see at once then there is a
one-to-one correspondence between the complex numbers and the points in the plane. In the usual
way, we can think of the sum of two complex numbers, the point in the plane corresponding to
z + w is the diagonal of the parallelogram having z and w as sides:

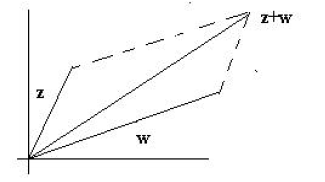
We shall postpone until the next section the geometric interpretation of the product of two complex
numbers.

The modulus of a complex number z = x + iy is defined to be the nonnegative real number
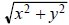, which is, of course, the length of the vector interpretation of z. This modulus is
traditionally denoted |z|, and is sometimes called the length of z. Note that 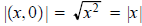and
so is an excellent choice of notation for the modulus.

The conjugate 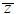of a complex number z = x + iy is defined by 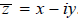. Thus .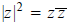
Observe that if z = x + iy and w = u + iv, then

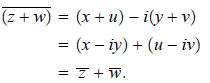
In other words, the conjugate of the sum is the sum of the conjugates. It is also true that .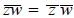
If z = x + iy, then x is called the real part of z, and y is called the imaginary part of z. These are
usually denoted Rez and Imz, respectively. Observe then that 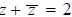Rez and 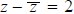Imz.

Now, for any two complex numbers z and w consider

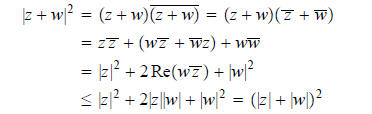
In other words,

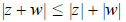
the so-called triangle inequality. (This inequality is an obvious geometric fact–can you guess why
it is called the triangle inequality?)

Exercises

4. a)Prove that for any two complex numbers,
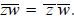
b)Prove that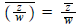

5. Prove that |zw| = |z||w| and that

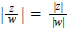
6. Sketch the set of points satisfying

Polar coordinates. Now let’s look at polar coordinates (r, θ) of complex numbers. Then we may
write z = r(cosθ + i sinθ). In complex analysis, we do not allow r to be negative; thus r is simply
the modulus of z. The number θ is called an argument of z, and there are, of course, many
different possibilities for θ. Thus a complex numbers has an infinite number of arguments, any two
of which differ by an integral multiple of 2π. We usually write θ = arg z. The principal argument
of z is the unique argument that lies on the interval

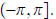
Example. For 1 - i, we have

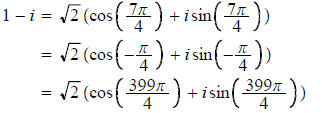
etc., etc., etc. Each of the numbers 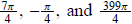is an argument of 1 - i, but the principal
argument is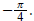

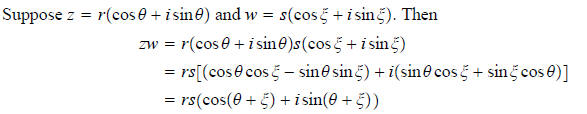
We have the nice result that the product of two complex numbers is the complex number whose
modulus is the product of the moduli of the two factors and an argument is the sum of arguments
of the factors. A picture:

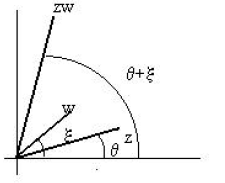
We now define exp(iθ), or 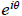by

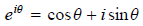
We shall see later as the drama of the term unfolds that this very suggestive notation is an excellent
choice. Now, we have in polar form

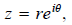
where r = |z| and θ is any argument of z. Observe we have just shown that

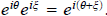
It follows from this that 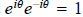. Thus

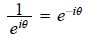
It is easy to see that

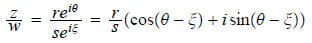
Exercises

7. Write in polar form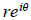

8. Write in rectangular form—no decimal approximations, no trig functions:

9. a) Find a polar form of
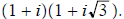
b) Use the result of a) to find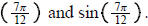

10. Find the rectangular form of

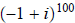
11. Find all z such that z^3 = 1. (Again, rectangular form, no trig functions.)

12. Find all z such that z^4 = 16i. (Rectangular form, etc.)

George Cain
School of Mathematics
Georgia Institute of Technology