ON SYSTEMS OF LINEAR DIOPHANTINE EQUATIONS
EXAMPLE. Solve the system of diophantine equations Ax = b, where
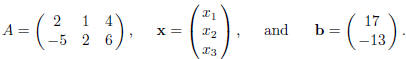
Solution. Consider a sequence of elementary
transformations of rows and columns of A. It is
well known that they can be achieved by multiplying A by unimodular matrices.
Let us represent the
transformation of rows by 2×2 matrices Li’s and the ones of columns by 3×3
matrices Rj ’s, where
the lower indices reflect the order of multiplications. We consider the
following transformations
(matrices):
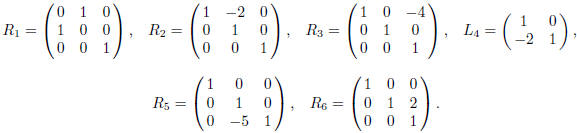
Let L = L4 and R = R1R2R3R5R6. Then
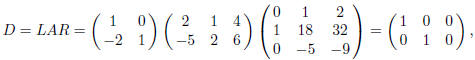
and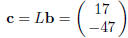 
.
Solving Dy = c, and taking x = Ry, we get
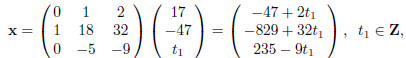
and the problem is solved.
Another application is concerned with a special instance of the following
fundamental question
in number theory. Let
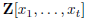denote the ring of polynomials in t
variables with integral
coefficients, and let
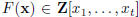. It is clear that if the equation F(x) = 0 has an integer
solution, then for any integer n ≥ 1, the congruence F(x) ≡ 0 (mod n) has a
solution. The
converse, in general, is false, even for the case of one variable. A simple
counterexample is provided
by F(x) = (2x+1)(3x+1). To show that (2x+1)(3x+1) ≡ 0 (mod n) has a solution,
write n in
the form n = 2a3bm, where gcd(m, 2) = gcd(m, 3) = 1, and a and b are nonnegative
integers. Then
use the Chinese Remainder Theorem. For more on the relation between congruences
and equations
see, e.g., [2]. Nevertheless the following is valid.
PROPOSITION 3. Let 
, and b ∈ Zn. Then the system of linear equations
Ax = b
has an integer solution if and only if the corresponding system of congruences
Ax ≡ b (mod n)
has a solution for every positive integer n.
Proof. Obviously, the first statement implies the second. Suppose the system of
congruences
has a solution for every positive integer n. Let L,R,D, y and c be as in
Proposition 2, and let N ∈ Z
be such that the transition from Ax = b to Dy = c uses
integers with absolute values smaller than
N. Then for every n ≥ N, Ax ≡ b (mod n) 
Dy
≡ c (mod n)
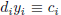(mod n),
i = 1, . . . , s. The latter system of congruences is solvable in particular
when n is a multiple of ds.
Since di | ds for every i, 1≤ i ≤ s, this implies
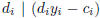, hence di | ci
for all i = 1, . . . , s.
Therefore Dy = c has an integer solution, and so does Ax = b.
The following statement allows one easily to compute the index of a subgroup of
the additive
group Zn, when the index is finite.
PROPOSITION 4. Let f : Zn → Zn be a Z–linear map and
be its matrix
with
respect to some choice of bases. Suppose A has rank n. Then the index of f(Zn)
in Zn is equal to
| detA |.
Proof. By Theorem 1 we can find two unimodular matrices L and R such that LAR =
D =
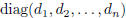. Since A is of rank n, all
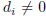. Therefore the abelian group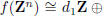 
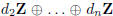, and the order of Zn/f(Zn)
is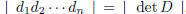
. Since
L and R are
unimodular, | detD | = | detA |.
EXAMPLE. Let f : Z2 → Z2 be defined by f((x, y)) = (28x + 38y, 12x + 16y).
Choosing both
bases to be the standard basis of Z2, we get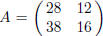 
.
Therefore the index [Z2 : f(Z2)] is
equal to | detA | = 8. The Smith normal form of A is
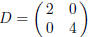, hence 
.
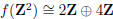Our next application is related to Proposition 4. It deals with some basic
notions of the
geometric number theory. Let R denote the field of real numbers, and
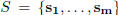be a
linearly independent set of vectors in Rn. The additive subgroup L =< S > of
Rn
generated by S
is called the lattice generated by S. A fundamental domain T = T(S) of the
lattice L is defined
as
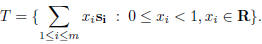
The volume v(T) of T is defined in the usual way, as the
square root of the absolute value of the
determinant of an m×m matrix whose i–th row is the coordinate vector of
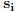in
the standard basis.
Though T itself depends on a particular set of generators of L, the volume of T
does not!
PROPOSITION 5. Let 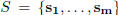and
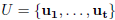be two sets of
linearly independent
vectors which generate the same lattice L. Then m = t and v(T(S)) = v(T(U)).
Proof. We leave it to the reader. In case of difficulties, look through [13, pp.
30-33 and
pp.168-169].
If one considers A with entries from a field, then by elementary operations of
rows and columns,
A can be brought to a diagonal form. It is a trivial exercise to check that an
elementary row (column)
operation preserves the dimensions of both row and column spaces of A. Therefore
matrices LAR
and A have equal dimensions of their row spaces and equal
dimensions of their column spaces. Since
the dimensions of row space and column space for a diagonal matrix are equal, we
have a proof of
the following fundamental result.
PROPOSITION 6. The dimension of row space of a matrix with entries from a field
is equal to
the dimension of its column space.
Acknowledgements. References [3], [11], and remarks concerning the algorithmic
aspects of finding the Smith
normal form of an integer matrix were kindly suggested to the author by an
anonymous referee. I am also very grateful to
Gary Ebert, Todd Powers, Andrew Woldar, the editor and referees, whose numerous
comments substantially improved the
original version of this paper.