Systems of Linear Equations
Markov Chains and
Dynamic Models
The refinery and economic supply-demand models of Section 1.2 were static
in the sense that we solved them once and that was it. There was one set of
production levels required, not a sequence of levels that would be needed
to describe an economy changing over time. A model that tries to predict
the behavior of a system over a period of time is called a dynamic model.
In this section we examine two dynamic linear models.
The first dynamic model we consider involves probability. This model,
called a Markov chain, will arise over and over in this book, so it is important
to understand the model well. The concepts of probability we need for this
model are simple and intuitive.
A Markov chain is a probabilistic model that describes the random
movement over time of some activity. At each period of time, the activity
is in one of several possible states. States might be amounts won in gam-
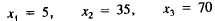
yield
heating oil = 520,
diesel oil = 890,
gasoline = 1040
This is getting quite close to our production goals. The overproduction
of 20 to 40 gallons in each product might be a reasonable safety margin
that is actually desirable.
To get closer, we should decrease x2 and x3 a little.
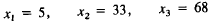
yield
heating oil = 504,
diesel oil = 852,
gasoline = 1006
This is an excellent fit. We have been a bit lucky. To do better, we
would probably have to use fractional values. (In the Exercises the
reader may need more tries to get this close.)
We next consider a slightly more complicated supply-demand model.
This model has the balancing advantage that trial-and-error calculations to
estimate a solution are easier. The reader is warned that it takes a little
while
to get a feel for all the numbers in this model.
Example 2. A Model of General Economic
Supply-Demand
We present a linear model due to W. Leontief, a Nobel Prize-winning
economist. The model seeks to balance supply and demand throughout
a whole economy. For each industry, there will be one supply-demand
equation. In practical applications, Leontief economic models can have
hundreds or thousands of specific industries. We consider an example
with four industries.
The left-hand side of each equation is the supply, the
amount
produced by the ith industry. Call this quantity xi; it is measured
in
dollars. On the right-hand side, we have the demand for the product
of the ith industry. There are two parts to the demand. The first part
is demand for the output by other industries (to create other products
requires some of this product as input). The second part is consumer
demand for the product.
For a concrete instance, let us consider an economy of
four general
industries: energy, construction, transportation, and steel. Suppose
that the supply-demand equations are
| Industrial Demands | ||||||
| Supply | Transport. | Energy | Construct. | Steel |
Consumer Demand |
|
| Energy: | x1= |
 |
||||
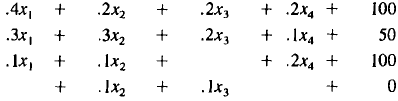| Construct.: | x2= | |||||
| Transport. : | x3= | |||||
| Steel: | x4= | |||||
(6)
The first equation, for energy, has the supply of energy x1
on the
left. The terms on the right of this equation are the various demands
that this supply must meet. The first term on the right, 4x1 is the
input of energy required to produce our x1dollars of energy (A units
of energy input for one unit of energy output). Also, the second term
of .2x2 is the input of energy needed to make x2 dollars
of construction.
Similarly, terms .2x3 and .2x4 are energy inputs required
for transportation
and steel production. The final term of 100 is the fixed consumer
demand.
Each column gives the set of input demands of an industry. For
example, the third column tells us that to produce the x3 dollars of
transportation requires as input .2x3 dollars of energy, .2x3
dollars of
construction, and .1x3 dollars of steel. In the previous refinery
model,
the demand for each product was a single constant quantity. In the
Leontief model, there are many unknown demands that each industry's
output must satisfy. There is an ultimate consumer demand for each
output, but to meet this demand industries generate input demands on
each other. Thus the demands are highly interrelated: Demand for
energy depends on the production levels of other industries. and these
production levels depend in turn on the demand for their outputs by
other industries, and so on.
When the levels of industrial output satisfy these supply-demand
equations, economists say that the economy is in equilibrium.
As in the refinery model, let us try to solve this system of equations
by trial-and-error. As a first guess, let us set the production levels
at twice the consumer demand (the doubling tries to account for the
interindustry demands). So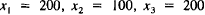 
, and
x4 = 0; these are our supplies. Given these production levels, we can
compute the demands from (6).
| Supply | Demand | ||
| Energy: | 200 |
 |
|
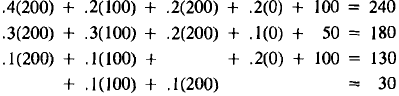| Construct.: | 100 | ||
| Transport.: | 200 | ||
| Steel: | 0 | ||
(7)
For our next approximations, let us try supply levels
halfway
between the supply and demand values in (7). That is,
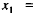
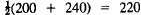, and similarly,
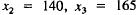, and
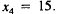
| Supply | Demand | |
| Energy: | 220 |  |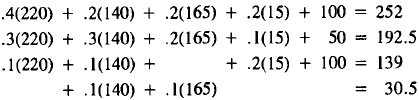
| Construct.: | 140 | |
| Steel: | 165 | |
| Steel: | 15 | |
(8)
The second approximation is only moderately better. The
interaction
effects between different industries are hard to predict. Adjusting production
levels was much easier in the refinery problem, where the
demand for each product was constant.
Let us stop trying to be clever and just use the
simple-minded
approach of setting production levels (i.e., supply levels) equal to the
previous demand levels. So from (8), we try
| Supply | Demand | |
| Energy: | 252 |  |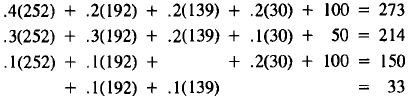
| Construct. : | 192 | |
| Transport. : | 139 | |
| Steel: | 30 | |
(9)
The demand values here have been rounded to whole numbers.
The
supplies and demands are getting a little closer together in (9).Repeating
the process of setting the new supply levels equal to the previous
demand levels (i.e., the demands on the right side in (9)) yields
| Supply | Demand | |
| Energy: | 273 |  |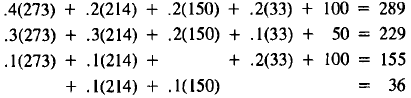
| Construct. : | 214 | |
| Transport. : | 150 | |
| Steel: | 33 | |
(10)
Repeating this process again, we have
| Supply | Demand | |
| Energy: | 289 |  |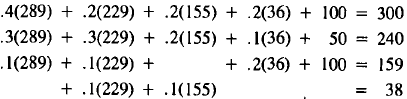
| Construct. : | 229 | |
| Transport. : | 155 | |
| Steel: | 36 | |
(11)
Observe that in successive rounds (9), (10), (11),
supplies are
rising. This is because as we produce more, we need more input which
requires us to produce still more, and so on. It may be that this iteration
will go on forever, and no equilibrium exists. On the other hand, the
gap between supplies and demands is decreasing.
Leontief proposed a constraint on the input costs that we
shall
show (in Section 3.4) guarantees that an equilibrium exists. The constraint
is
Input Constraint. Every industry is profitable:
Every industry must
require less than $1 of inputs to produce $1 of output.
In mathematical terms, this means that the sum of the
coefficients
in each column must be less than I. Our data in (6) satisfy this constraint,
so an equilibrium does exist for this four-industry economy.
Moreover, the iteration process of repeatedly setting production levels
equal to the previous demands will converge to this equilibrium. The
reader should check that the following numbers are equilibrium values
(rounded to the nearest integer).
Equilibrium: energy = 325, construction = 265,
transportation = 168, steel = 43
Note that any system of linear equations can be rewritten
in the form
of supply-demand equations with xi appearing alone on the left side of the
ith equation, as in the Leontief supply-demand model (6). It is standard
practice to solve large systems of linear equations by some sort of iterative
method. The nature of the supply-demand equations suggested the iterative
scheme we used here, letting the demands from one round be the production
levels of the next round .