Rational Functions

Recall from Section 1.2 that an even function is
symmetric with respect to the y-axis, and an odd
function is symmetric with respect to the origin. This
can sometimes save time in graphing rational
functions. If a function is even or odd, then half of the
function can be graphed, and the rest can be graphed
using symmetry.

Determine if the functions below are even, odd, or
neither.

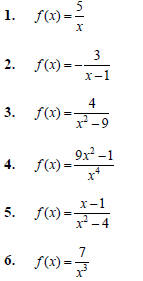
In each of the graphs below, only half of the graph is
given. Sketch the remainder of the graph, given that
the function is:
(a) Even
(b) Odd

(Notice the asymptotes at x = 2 and y = 0 .)

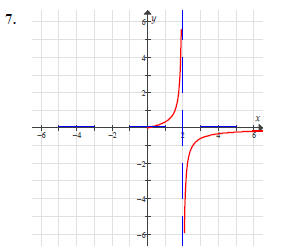
(Notice the asymptotes at x = 0 and y = 0 .)

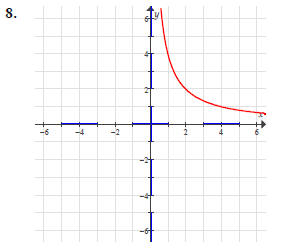
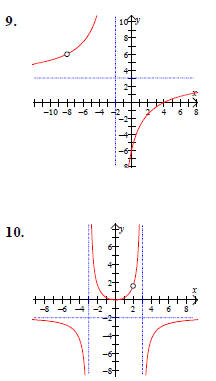
For each of the following graphs:
(a) Identify the location of any hole(s)
(i.e. removable discontinuities)
(b) Identify any x-intercept(s)
(c) Identify any y-intercept(s)
(d) Identify any vertical asymptote(s)
(e) Identify any horizontal asymptote(s)

For each of the following rational functions:
(a) Find the domain of the function
(b) Identify the location of any hole(s)
(i.e. removable discontinuities)
(c) Identify any x-intercept(s)
(d) Identify any y-intercept(s)
(e) Identify any vertical asymptote(s)
(f) Identify any horizontal asymptote(s)
(g) Identify any slant asymptote(s)
(h) Sketch the graph of the function. Be sure to
include all of the above features on your
graph.

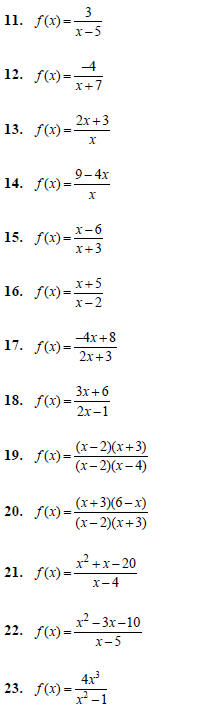
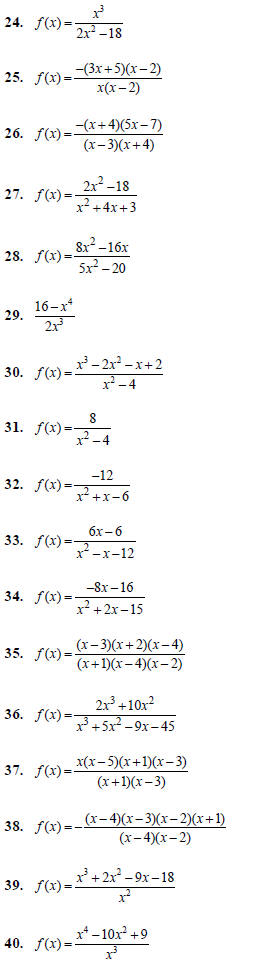
Answer the following.

41. In the function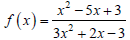

(a) Use the quadratic formula to find the x-intercepts
of the function, and then use a
calculator to round these answers to the
nearest tenth.

(b) Use the quadratic formula to find the
vertical asymptotes of the function, and then
use a calculator to round these answers to
the nearest tenth.

42. In the function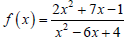

(a) Use the quadratic formula to find the x-intercepts
of the function, and then use a
calculator to round these answers to the
nearest tenth.

(b) Use the quadratic formula to find the
vertical asymptotes of the function, and then
use a calculator to round these answers to
the nearest tenth.

The graph of a rational function never intersects a
vertical asymptote, but at times the graph intersects a
horizontal asymptote. For each function f ( x) below,

(a) Find the equation for the horizontal
asymptote of the function.

(b) Find the x-value where f ( x) intersects the
horizontal asymptote.

(c) Find the point of intersection of f ( x) and
the horizontal asymptote.

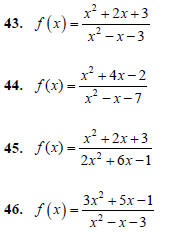
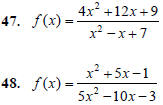
Answer the following.
49. The function 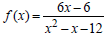was graphed in
Exercise 33.

(a) Find the point of intersection of f (x) and
the horizontal asymptote.

(b) Sketch the graph of f (x) as directed in
Exercise 33, but also label the intersection of
f ( x) and the horizontal asymptote.

50. The functio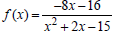n was graphed in
Exercise 34.

(a) Find the point of intersection of f (x) and
the horizontal asymptote.

(b) Sketch the graph of f (x) as directed in
Exercise 34, but also label the intersection of
f ( x) and the horizontal asymptote.