Algebra of Functions
Objectives
 To define the sum, difference, product, and
quotient
To define the sum, difference, product, and
quotient
of functions.
 To form and evaluate composite functions.
To form and evaluate composite functions.
Basic function operations
 Sum
Sum 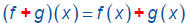
 Difference
Difference 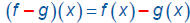
 Product
Product 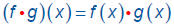
 Quotient
Quotient 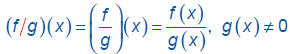
Function, domain, & range
 The domain of a function is the set of all “first
The domain of a function is the set of all “first
coordinates” of the ordered pairs of a relation.
 The range of a function is the set of all “second
The range of a function is the set of all “second
coordinates” of the ordered pairs of a relation.
 A relation is a function if all values of the domain are
A relation is a function if all values of the domain are
unique (they do not repeat).
 A test to see if a relation is a function is the
vertical
A test to see if a relation is a function is the
vertical
line test.
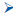 If it is possible to draw a vertical line and cross the graph
If it is possible to draw a vertical line and cross the graph
of a relation in more than one point, the relation is not
a function.
Example 1
 Find each function and state its domain:
Find each function and state its domain:
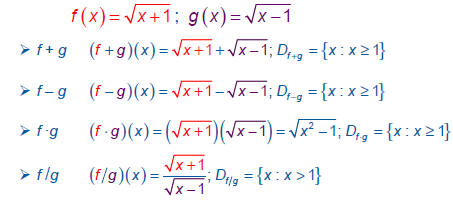
Example 2
 The efficiency of an engine with a given heat output,
The efficiency of an engine with a given heat output,
in calories, can be calculated by finding the ratio of
two functions of heat input, D and N, where
| D(i) = i – 5700 and N(i) = i . | ||
 |
 Write a function for the efficiency of Write a function for the efficiency of the engine in terms of heat input (i), in calories. |
 |
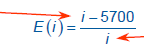 |
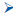 Find the efficiency when the heat input is 17,200 calories.
Find the efficiency when the heat input is 17,200 calories.
Composition of functions
 Composition of functions is the successive
Composition of functions is the successive
application of the functions in a specific order.
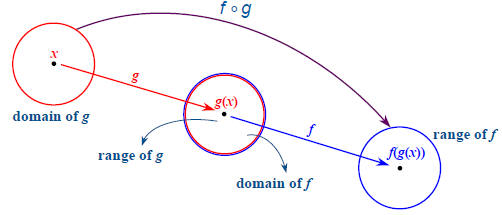
 Given two functions f and g, the composite function
Given two functions f and g, the composite function
is f o g defined by 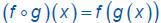 and is read
and is read
“f of g of x.”
 The domain of is f o g the set of elements x in the
The domain of is f o g the set of elements x in the
domain of g such that g(x) is in the domain of f.
 Another way to say that is to say that “the range of function
Another way to say that is to say that “the range of function
g must be in the domain of function f.”
A composite function
Example 3
 Evaluate ( f o g ) ( x ) and ( g o f ) ( x ) :
Evaluate ( f o g ) ( x ) and ( g o f ) ( x ) :
f (x) = x − 3
g (x) = 2x2 −1
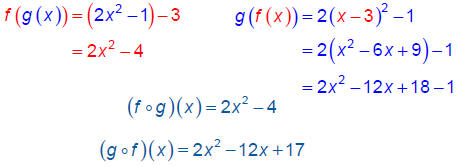
 You can see that function composition is not
You can see that function composition is not
commutative!
Example 4
 Find the domain of
Find the domain of
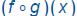 and
and 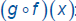
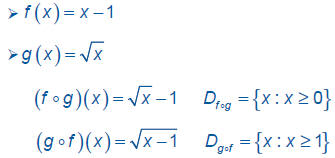
(Since a radicand can’t be negative in the set of real
numbers, the radicand must be greater than or equal to
zero. This is what limits the domain.)
Example 5
 The number of bicycle helmets produced in a factory
The number of bicycle helmets produced in a factory
each day is a function of the number of hours (t) the
assembly line is in operation that day and is given by
n = P(t) = 75t – 2t2.
 The cost C of producing the helmets is a function of
The cost C of producing the helmets is a function of
the number of helmets produced and is given by
C(n) = 7n +1000.
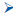 Determine a function that gives the cost of producing the
Determine a function that gives the cost of producing the
helmets in terms of the number of hours the assembly line is
functioning on a given day.
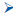 Find the cost of the bicycle helmets produced on a day
Find the cost of the bicycle helmets produced on a day
when the assembly line was functioning 12 hours.
(solution on next slide)
C(n) = 7n + 1000
n = P (t ) = 75t − 2t2
Solution to Example 5:
 Determine a function that gives the cost of producing
Determine a function that gives the cost of producing
the helmets in terms of the number of hours the
assembly line is functioning on a given day.
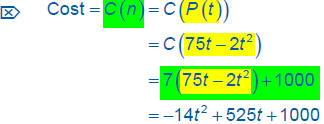
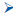 Find the cost of the bicycle helmets produced on a day
Find the cost of the bicycle helmets produced on a day
when the assembly line was functioning 12 hours.
Review
 If f ( x ) = 2 x + 1 a n d g ( x ) = x2 , find f (g (x)).
If f ( x ) = 2 x + 1 a n d g ( x ) = x2 , find f (g (x)).
 Find g (f (x)).
Find g (f (x)).
 What is the domain of g (f (x ))?
What is the domain of g (f (x ))?
 Consider the functions
Consider the functions
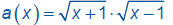
and 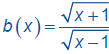 Why are their domains different?
Why are their domains different?
Answers to review:
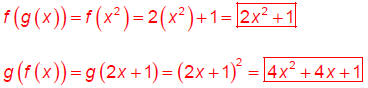
Domain of g (f (x)) is {x : x ∈ }
}
The domains of the two functions are different because
the denominator of b(x) cannot be zero.
Summary…
 Function arithmetic – add the functions (subtract, etc)
Function arithmetic – add the functions (subtract, etc)
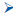 Addition
Addition
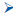 Subtraction
Subtraction
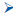 Multiplication
Multiplication
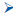 Division
Division
 Function composition
Function composition
 Perform function in innermost parentheses first
Perform function in innermost parentheses first
 Domain of “main” function must include range of “inner”
Domain of “main” function must include range of “inner”
function


