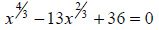Algebra Review
INTEGER EXPONENTS
The basic laws for working with exponents are

Example: Simplify (x2 )3 - x2
(x4 + x3 )
Solution:
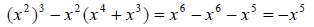
Example: Eliminate negative exponents and simplify
(3x8y-6)(-5x-4y6).
Solution:
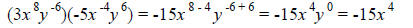
Example: Eliminate negative exponents and simplify
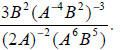
Solution:
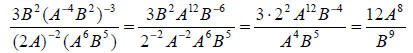
Example: Eliminate negative exponents and simplify
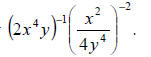
Solution:
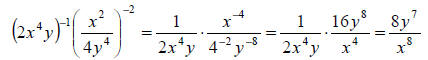
Problems: Eliminate negative exponents and
simplify.
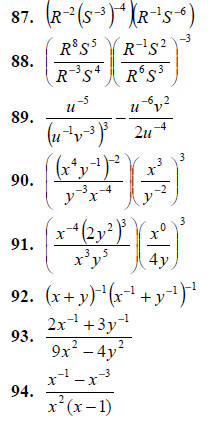
RATIONAL EXPONENTS AND RADICALS
Recall that for a > 0 and n a positive integer,
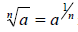 means a positive number b such that b^n = a.
It follows that
means a positive number b such that b^n = a.
It follows that 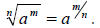
Thus, radical expressions can be converted to expressions involving fractional
exponents. These fractional exponents obey the
same laws as integer exponents previously
reviewed. For instance,
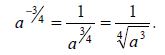
A word of warning! 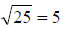 , not
, not
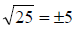 .
.
Example: Simplify by expressing radicals as
non-negative rational powers and combining powers
whenever possible: 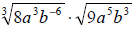
Solution:
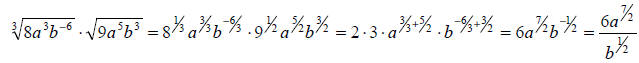
Problems: Simplify by expressing radicals as non-negative rational powers
and combining powers
whenever possible.
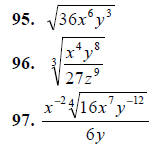
For typographical convenience and historical reasons, it is customary to write
expressions involving both fractions and radicals
so that no fraction appears under a radical sign and no radical appears in a
denominator. This "rationalizing the denominator"
is accomplished in several ways, as illustrated in the following examples.
Example:
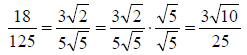
Example:
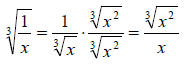
Example:
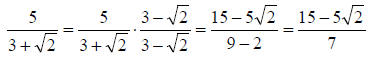
Example:
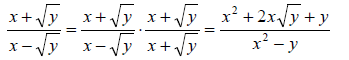
Problems:
98. Rationalize the denominator in
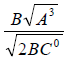 .
.
99. Rationalize the denominator in 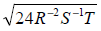 .
.
100. Rationalize the denominator in 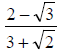 .
.
101. Rationalize the denominator in 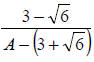 .
.
SOLVING RADICAL EQUATIONS
Equations involving radicals are often solved by rewriting
the equation, raising both sides to some
power to remove the radical, and then solving the resulting equation. As with
fractional equations, this
process may introduce extraneous roots. Potential solutions must be checked in
the original equation.
Example: Solve for x:
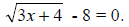
Solution:
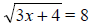
Squaring both sides we get 3x + 4 = 64,
so 3x = 60.
Thus, x = 20 is a possible solution.
Checking in the original equation we find 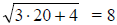 .
Thus x = 20 is the solution.
.
Thus x = 20 is the solution.
Example: Solve for x:
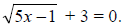
Solution:
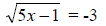
Squaring both sides we get 5x - 1 = 9,
so 5x = 10.
Thus, x = 2 is a possible solution.
Check in the original equation and find 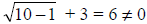 .
(Recall that § means nonnegative
.
(Recall that § means nonnegative
square root!) Thus, x = 2 is not a solution. This equation has no solution.
Example: Solve for y:
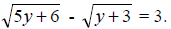
Solution:
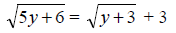
Square both sides and find
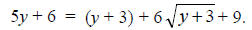
Isolate the square root term to get
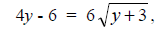
and square again to get
16y2 - 48y + 36 = 36y + 108.
We find
16y2 - 84y - 72 = 0,
or 4y2 - 21y - 18 = 0,
so y = -3/4 or 6.
Checking by substituting into the original equation, we
find that 6 is a solution and -3/4
is not. The only solution is y = 6.
Problems:
102. Solve for x: 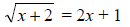
103. Solve for x: 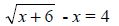
104. Solve for x: 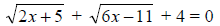
105. Solve for x: 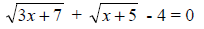
POWER FUNCTIONS
A function, f (x) = x^a where a is a real number is called a power function. You
have already worked
with many power
functions including functions like
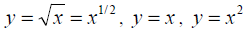 ,
,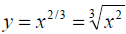 .
.
Example:
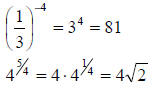
Example: Solve for x: x3/2 = 27
Solution:
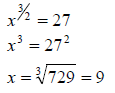
Example: Solve for x: 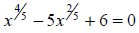
Solution:
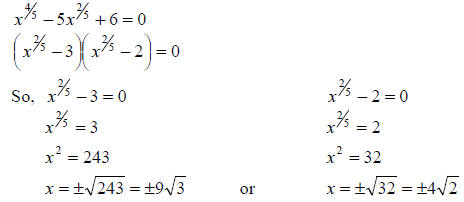
Problems:
106. Solve for x: 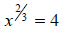
107. Solve for x: 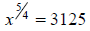
108. Solve for x: 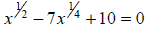
109. Solve for x: