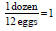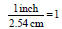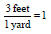What is Chemistry?
| Chapter 1 Chemistry: Matter and Measurement |
What is Chemistry? • On your note card, write your name at the top and numbers 1 - 4 down the left side. When each word is shown below, write the first thing that comes to mind. • 1) Chemistry • 2) Chemicals • 3) Science • 4) Experiments |
| Things You Should Know… • Names of rows in the Periodic Table (periods) and columns (groups) • Names of the 4 main groups • Names of the 3 general types of elements (metals, nonmetals, metalloids) • SI units:  |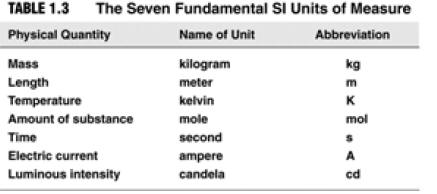
Things you should know… • Names and symbols of elements: • Numbers 1 – 38, Cs, Ba, Hg, Ag, Au, Sn, Pb • Zn2+, Cd2+, Ag1+ |
| Things you should know…. • Lab equipment  |
Measurements • Temperature  K, °C, °F K = °C + 273.15F = (9/5 * °C) + 32°F• C = 5/9 * (°F – 32) • Volume mL = cm3,
L = dm3 |
Elements and the Periodic Table |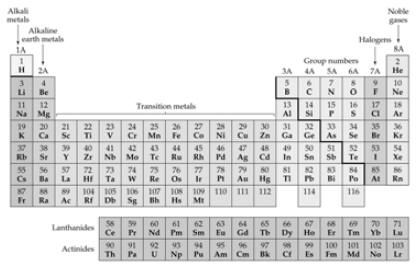
The Periodic Table |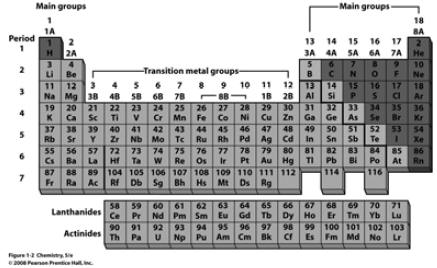
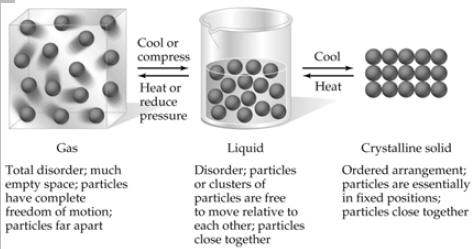
| States of Matter
|
Physical and Chemical Changes • What is happening below? 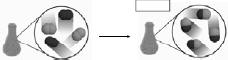 • Is this a physical or chemical change? • What’s the difference between the two? • Boiling water: physical or chemical? • Lighting a hydrogen |
| Physical or Chemical Change? • Do the following equations represent a physical or a chemical change? How can you tell?  |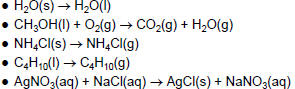
Density • D = m / v • Mass per volume Greater mass (same vol.) = more denseGreater volume (same mass) = less dense• Diet versus regular coke • If a steel ball bearing weighs 54.2 grams and has a volume of 6.94 cm3, what is its density? • If a steel beam is measured to have a volume of 94390 cm3, how much does it weigh? |
| Density • Carbon dioxide gas is more dense than helium gas. Use the pictures below to explain why.  |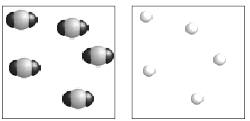
Scientific Notation • Use scientific notation to describe very large or very small numbers. • Negative exponents indicate small number, positive exponents indicate large number. • How can we describe the size of an atom? The size of the universe? • Scientific notation and powers of ten • Powers of Ten |
| Scientific Notation • Write the following numbers in scientific notation and place in order of increasing value: • 10, 0.001, 0.00002, 1 x 104, 1 x 10-3, 3 x 10-5, 8 x 105, 700000 • Add, multiply, and divide 3 x 103 and 2 x 102 |
How to Use Your Calculator • To enter 1.00 x 104 in your calculator, DO NOT enter “x” or “10”. • Instead, use the exponent key (“EXP” or “EE”). • Press: 1.00 “EXP” (or “EE”) 4 |
| Scientific Notation Practice • Add 3.0 x 103
+ 2.0 x 102• Multiply (3 x 103)(2 x 102) = (3 * 2) x (103 * 102) Add exponents•Divide (3.0 x 103) / (2.0 x 102) = (3.0 / 2.0) * (103/102) = Subtract exponents (top – bottom)• Adding and subtracting exponents is a good way to estimate answers to problems!! |
Scientific Notation Practice • Addition and Subtraction • Combine numbers with same exponent and add numbers • 7.4 x 103 + 2.1 x 103 = 9.5 x 103 • Multiplication • Add exponents and multiply numbers • 8.0 x 104 * 5.0 x 102 = 40 x 106 = 4.0 x 107 • Division • Subtract exponents and divide numbers • 6.9 x 107 / 3.0 x 10-5 = 6.9/3.0 x 107-(-5) = 2.3 x 1012 |
| Uncertainty in Measurement • What is the difference between precision and accuracy? What is shown in each picture below?
|
Uncertainty in Measurement • The true temperature outside is 71.2oF. Several thermometers made by one manufacturer record the temperature as 67.8, 68.2, 67.2, 67.6, and 68.0oF. • How would you describe this data in terms of accuracy and precision? Why? |
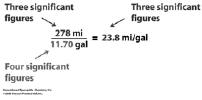
| Significant Figures • What are significant figures? • Why are they important? • When do you need to worry about them? • How many decimal places can you use on the rulers below (shown in cm)?  |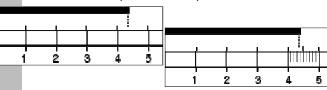
Significant Figures • Measurements versus calculations: In lab, sig figs are determined by the measuringdevice. When measuring volume, you can always estimate1 decimal place past the smallest increment. In class, sig figs are determined by given numbers. Sig figs for calculations are determined by thenumbers reported. There are rules for determining sig figs based oncalculations. |
| Sig Figs • Measuring volumes  |
Determining Significant Figures • All non-zero digits are significant (335 cm). • Zeroes in the middle of a number are significant (3406 mg). • Zeroes at the beginning of a number are NOT significant (0.000345 km). • Zeroes at the end of a number and after the decimal point are significant (43.21000 g). • Zeroes at the end of a number and before the decimal point may or may not be significant (5280 ft). You will have to look at the measurement to determine this. |
| Determining Significant Figures • How many significant figures are in the following? •1.45 • 0 38 •0.0670 • 301.9 • 072.8 • 1.0 • 44.20 •278 • 1098.40 •0.00041560 • 98.76 • 100 • 190 • 1.90 x 103 • 1063 • Hint: Write numbers in scientific notation to help determine if leading zeros are significant. |
Significant Figures in Calculations • Don’t round for sig. figs. until the END of all calculations. • Multiplication and division: report to the least number of significant figures. Ex: 2.8 x 4.5039 → 2 sig. figs. in answer= 12.61092 → 13 • Addition and subtraction: report to the least number of decimal places. Ex: 2.097 – 0.12 → 2 digits after decimal= 1.977 → 1.98 |
| Sig Figs in Calculations
• Multiplication |
Significant Figures Practice • Calculate the following: • 1.67890 x 56.32 • 9.0210 + 856.1 • (6.02 + 1.5) x (3.14 + 2.579) |
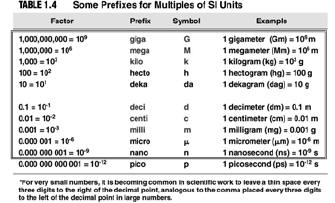
| Experimentation and Measurement • Metric prefixes
|
Dimensional Analysis • Allows us to convert from one unit to another • 1 dozen eggs = 12 eggs
• 1 inch = 2.54 cm
• 3 feet = 1 yard
|
| Metric Conversions • How many m are in 756 nm? • How many kg are in 12.34 g? • How many mL are in 1.450 L? • How many g are in 1907.12 mg? • How many mm are in 1.903 x 1010 m? |
Dimensional Analysis • A piece of string measures 5.5 inches long. How long is the string in mm? • 1 inch = 2.54 cm (will be given) •100 cm = 1 m (you need to know) • 1000 mm = 1 m (you need to know) |
| Dimensional Analysis Practice • Problem 1.17: Gemstones are weighed in carats, with 1 carat = 200 mg (exactly). What is the mass, in grams, of the Hope Diamond, the world’s largest blue diamond at 44.4 carats? • The density of a steel ball bearing is 7.81 g/cm3. If the ball bearing is measured to have a volume of 1.34 cm3, what is its mass in milligrams? |
