Math 102 Midterm Test

1. Find the quotient and reminder using long division.
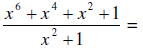quotient = x⁴ + 1 and the remainder is zero

2. Find the quotient using the synthetic division
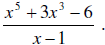quotient is x⁴ + x³ + 4x² + 4x + 4 and the remainder is

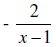
3. List all the possible rational zeros given by the Rational Zeros Theorem.
T(x) = 12x⁵ + 6x³ + 2x – 8
Let p = -8 and q = 12.
The factors of 8 are ± {1, 2, 4, 8} and the ones for 12 are ± {1, 2, 3, 6, 12}
Therefore the possible zeros are


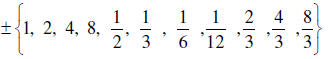
4. Use Descartes’ Rule of Signs to determine how many positive and how many
negative real zeros the polynomials can have. Then determine the possible total
number of real zeros.
P(x) = x⁵ - 4x³ – 5x² + 6x

The polynomial has two variations in sign, therefore it has either two or zero positive
zeros.
P(–x) = –x⁵ + 4x³ – 5x² – 6x

The polynomial has two variations in sign; therefore it has either two or zero negative
zeros.
Thus P(x) has a total of either four or two real zeros.

5. Find a polynomial with integer coefficients that satisfies the given conditions.
R has degree 4, and zeros 1 – 2i, and 1 with multiplicity 2.
(x – 1 – 2i)( x – 1 + 2i)(x – 2)(x – 2)
((x – 1) – 2i)(( x – 1) + 2i)(x – 2)(x – 2)
((x – 1)² – (2i)²)(x – 2)(x – 2)
((x – 1)² + 4)(x – 2)(x – 2) …

6. Sketch the graph of the function by making a table of values.
f(x) = 3^x Please see page 377 of our book.

7. Use the definition of the logarithmic function to find x.
log₅ 3125 = x
3125 = 5^x
5⁵ = 5^x
Therefore since the bases are the same we have that x = 5

8. Use the Laws of Logarithms to expand the expression.


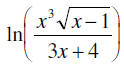
ln x³ + 1/2ln(x – 1) – ln(3x + 4)

9. Use the Laws of Logarithms to combine the expression.
ln 5 + 2ln x – 1/3ln(x² + 5)


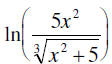
10. Solve the equation
e^4x + 4e^2x – 21 = 0
(e^2x – 3) (e^2x + 7) = 0
We have that either e^2x – 3 = 0 or e^2x + 7 = 0
So we have that e^2x = 3 or e^2x = – 7
But e^2x can not be negative. Therefore we have that e^2x = 3
So ln e^2x = ln3. So we have 2x = ln 3 then x = (ln3)/2

11. Solve for x.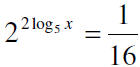
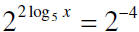Since the bases are the same
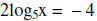
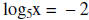then we have x = 5^-2 or x = 1/25

12. Solve the logarithm equation for x.

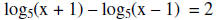
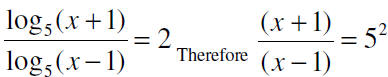
where x can not be equal to 1.
So 5² (x – 1) = X + 1 to obtain 5² x – 25 = x + 1 then 25x – x = 26 so we have x = 13/12

13. Write the augmented matrix of the system of equations
6x – 5y – z = - 2
x + -3y = 1
x – 2y + 4z = -2


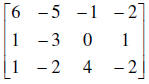
14. Given the following matrix, please explain the steps necessary to make the entry
in parenthesis equal to zero.


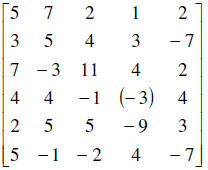
Many ways to do it. The easiest would be to add row 4 and row 2 to obtain our
new row 4. R₄ + R₂

15. Find the first four terms for the sequence a_n= 2a_n-1 + 1 and a₁ = 1

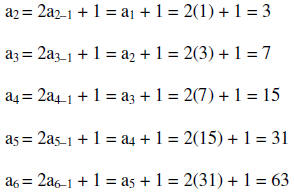
16. Find the first four terms for the sequence a_n= a_n-1 + a_n-2 and a₁= 1, and a₂ = 2

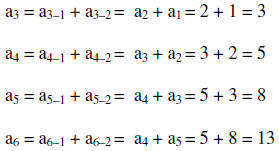
17. Find the nth term of the sequence whose first several terms are given

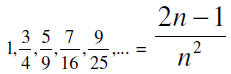
18. Find the first six partial sum s₁, s₂, s₃, s₄, s₅, s₆ of the sequence

,

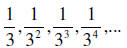
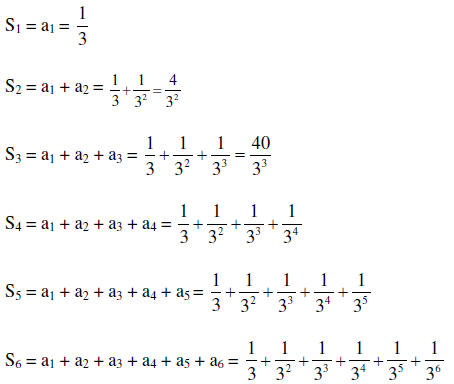
19. Find the first partials sum and the nth partial sum of the sequence

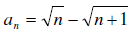
First let us list the first few terms

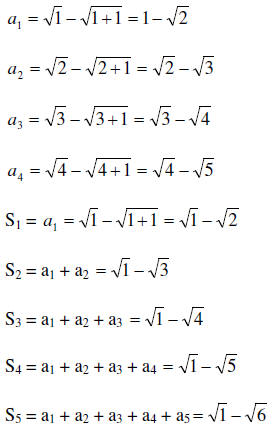
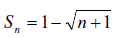
20. Factor the following polynomial
4x² - 20x + 24 = 4(x – 2)(x – 3)