Today´s Goal: We describe various methods to factor
algebraic expressions (specifically
polynomials) as a product of simpler ones.
Assignments:Homework(Sec.P.6)#3,6,9,15,17,21,27,31,38,39,47,53,61,77
(pp.48-50).
We have used the distributive property to "expand" algebraic
expressions (see Activity 5).
We sometimes need to reverse this process by "factoring" an expression as a
product of simpler ones.

Common Factors: The easiest type of factoring occurs when
the terms have a common factor.
Example 1: Factor out the common factor in each of the following expression:
![]()

Factoring Trinomials: To factor a trinomial of the form

we need to choose numbers r and s so that r + s = b and r s = c .
Example 2: Factor the following trinomials:
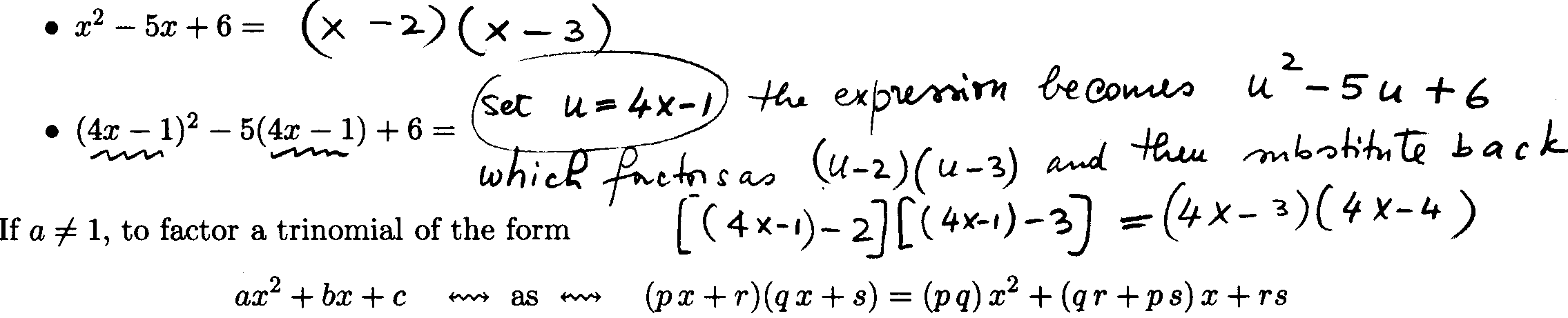
we need to choose numbers p, q, r and s so that p q = a, r s
= c, and q r + p s = b.
That is, p and q are factors of a whereas r and s are factors of c.
Example 3: Factor the following trinomial:

Special Factoring Formulas:
The first three formulas below are simply Special Product
Formulas written backward.
If A and B are any real numbers or algebraic expressions, then:

Example 4: Use a Factoring Formula to factor the following expressions:

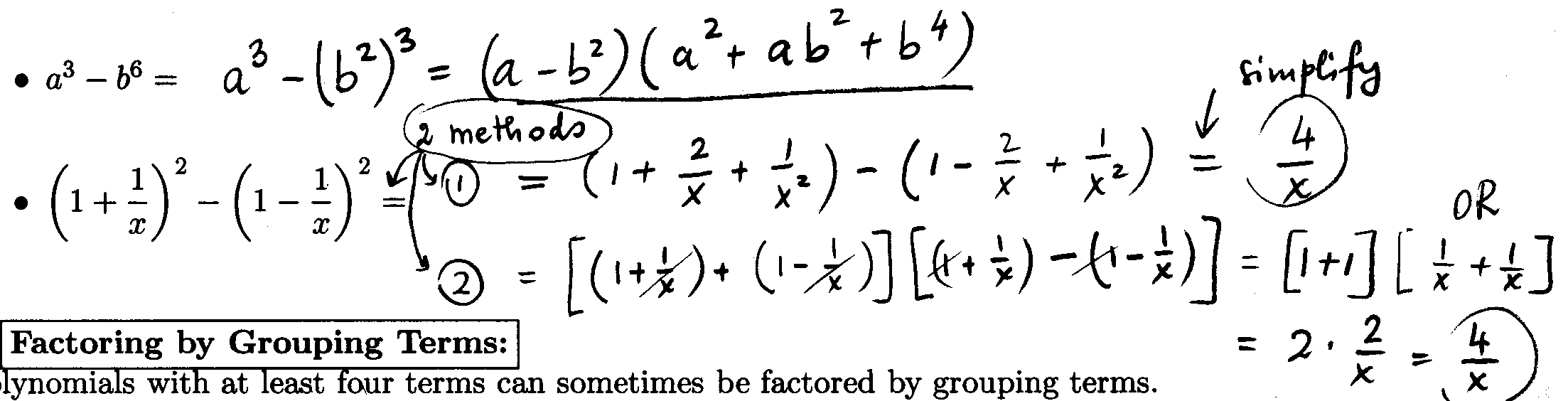
Factoring by Grouping Terms:
Polynomials with at least four terms can sometimes be
factored by grouping terms.
Example 5: Factor the following expressions by grouping terms:

Factoring an Expression Completely:
When we factor an expression, the result can sometimes be
factored further. We repeatedly use the methods
outlined in this activity until we have factored our algebraic expression
completely.
Example 6: Factor the following expressions completely:
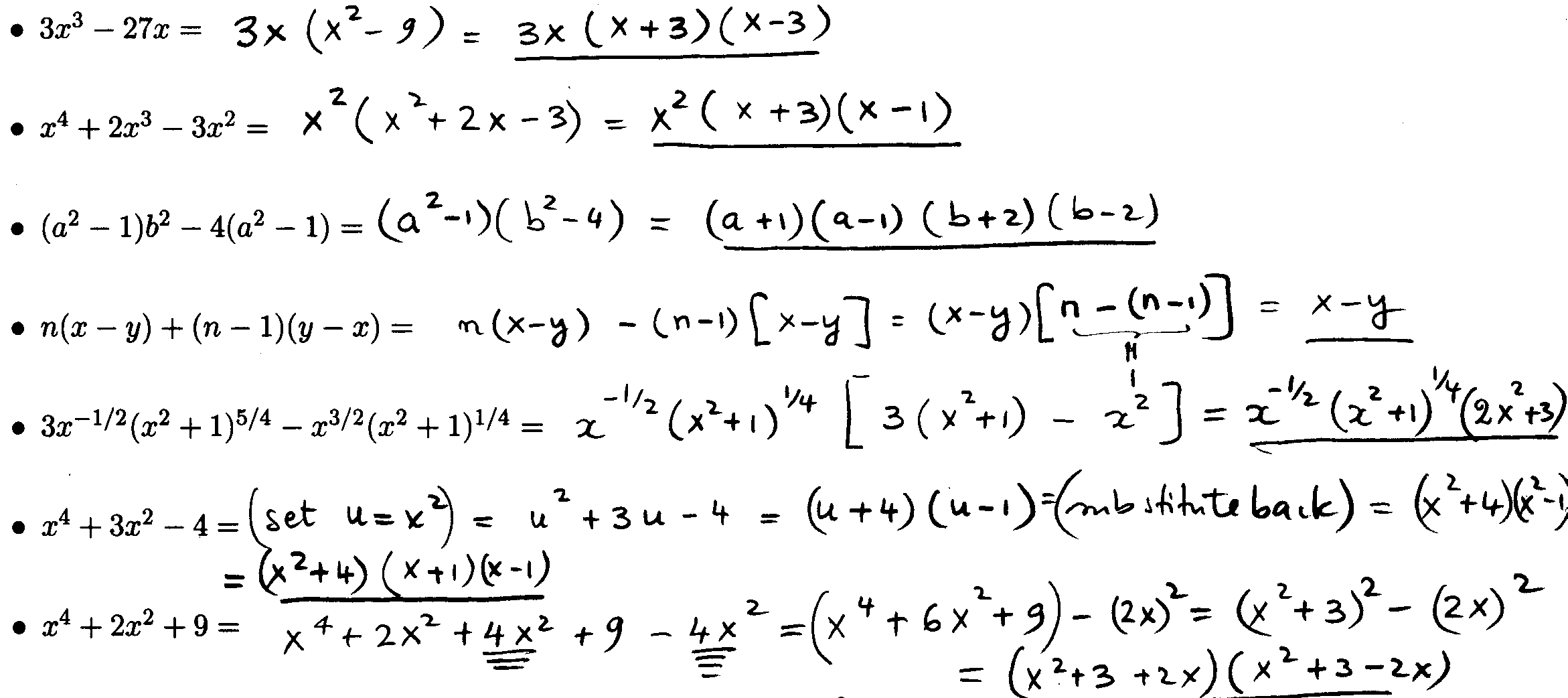
This last problem is trickier! (Hint: add and subtract "4x2" what do you obtain?)
Example 7 (Mowing a Field):
A square field in a certain state park is mo wed around the
edges every week. The rest of the field is kept
unmowed to serve as a habitat for the birds and small animals. the field
measures b feet by b feet, and the mowed
strip is x feet wide.

(a) Show that the area of the mowed portion is b2-(b-2x)2.
![]()
(b) Factor the expression in (a) to show that the area of the mowed portion is also 4x(b-x).



