Least Square
1 Description and Objectives
In this (our final) lab, you will put together many of the matrix operations
that you have
learned to produce an application that can solve Least Squares problems from
scratch.
This is a farily involved lab. (Sorry.) But on the bright side, you will have a
good while to
finish it.
Lab Objectives
1. Understand DenseMatrix class operations from previous lab.
2. Implement a Cholesky Factorization routine for solving (dense) symmetric
positive definite
linear systems
3. Understand how to use the Cholesky Factorization to solve a linear system
4. Learn how to create the normal equations that are required for a least
squares curve
fitting, including operations for matrix transpose
5. Solve the linear system(s) necessary to perform a least-squares curve fitting
2 Cholesky Decomposition
Our first step towards our goal of having a least squares solver is to build a
class that can
factorize a symmetric positive definite matrix into lower and upper triangular
parts: A =
LLT . All of the operations today will use (and extend) the DenseMatrix classes
you wrote
for Lab 11.
2.1 Problem
Implement the constructor for the CholeskyDecomposition class I gave you. You
may wish
to use the matrix in the file C1.txt, which has a decomposition:
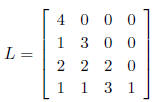
3 Solving Linear Systems
3.1 Problem
Write a solve method for the CholeskyDecomposition class that takes a
DenseMatrix
as input and outputs a DenseMatrix as the solution to the matrix system
AX = B
The pseudocode TriangularSolve given in class today should come in quite handy.
You can
use the file RHS.txt, which has b = [32, 26, 38, 30]T You can (if you wish)
assume that B has
only one column (and then so would the matrix returned by your method) Note
however, that
this is not necessary...
4 Useful Code
4.1 Problem
Write a (simple) method for your DenseMatrix class that returns a copy of the
transpose of
the matrix
5 Least Squares
You are a master brewmaker, and you would like to form a functional relationship
to help you
predict the “yummyness” of a beer y as a function of the amount of hops x you
put in the beer.
Your experiments yielded the measures given in Table 1, as well as hours of
enjoyment:
Table 1: Measurements of Yummyness
| Hops | Yummyness |
 |
|
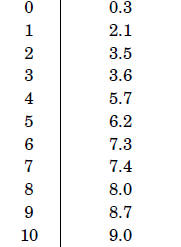5.1 Problem
Using the codes you have developed, compute a best linear fit for these
measurements: y =
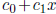. What are the coefficients
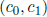? Plot the data as well as your (linear)
approximation
to it.
5.2 Problem
Using the codes you have developed, compute a best quadratic fit for these
measurements: y =
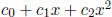. What are the coefficients
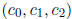? Plot the data as well as your (quadratic)
approximation to it.
6 Bonus Problem
6.1 Problem
Let e(n) be the total error in the approximation (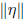
)
if a basis of polynomials up to degree
n − 1 is used. Plot e(n) as a function of n for the data in Table 1
7 Lab Deliverables
• Three files: Lab12.java, DenseMatrix.java, CholeskyDecomposition.java. You
should not have to change (too much) the code in Lab12.java, though you may find
it
useful to comment parts out while you do the code development. Also, your
estimates
and plots for the problems in Section 5.
8 Problem Set (In addition to those from Lab11)
8.1 Problem
CLRS 28.5-6
8.2 Problem
For the following two matrices, provide a Cholesky decomposition, or prove that
the matrix is
not SPD
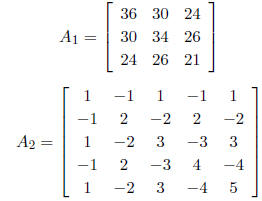
8.3 Problem
28-1 (a), (b), (c).
8.1 Extra Credit
8.4 Problem
28-1 (d) (e)