Algebra Review Lessons
Lesson 1 Laws of Exponents: Product Laws
We know that 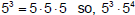 so,
so,
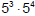 would be
would be 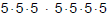 or
or 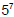
There is a short cut here that becomes our first Product Law of Exponents:
| Exponent Law 1: For any real numbers a, m, and n: 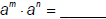 |
Simplify the following:
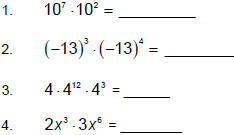
Taking this idea a step farther….what happens if we have:
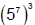 ?
?
That would mean, _____· _____ · _____ or 5____
Perhaps you see another law at work here…
| Exponent Law 2: For any real numbers a, m, and n: 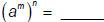 |
Similarly, when there is a product inside the parentheses,
you raise each term to the outside
exponent…
| Exponent Law 3: For any real numbers a, b, k, and m: 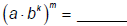 |
Simplify:

Lesson 2: Laws of Exponents: Quotient Laws
If, instead of multiplying, we divided,
then…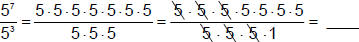
So, looking at the exponents so you see a short cut? This becomes another law of exponents.
| Exponent Law 4: For any real numbers a, k, and m (where a ≠0): 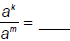 |
Look what happens when we apply this law to this situation:
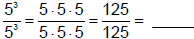 Now by the law of
exponents ,
Now by the law of
exponents ,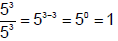
So we know that any real number raised to the zero
power equals 1. (Corollary to Law 4)
Another helpful law of exponents is:
| Exponent Law 5: For any real numbers a, b, and m, where b≠ 0: 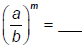 and and
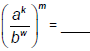 |
Simplify:

There is a situation where using the laws of exponents is dangerous. Let’s look at that now.
Lesson 3 Laws of Exponents: Negative Exponents
Consider,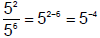 but what does this mean? Doing this
the long way we see that
but what does this mean? Doing this
the long way we see that
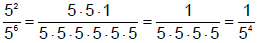 This tells us
This tells us
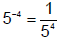
In general, this law of negative exponents is:
| Exponent Law 6: For any real numbers x and m where x ≠ 0 : 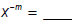 and
and 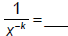 |
The danger is two-fold. When you look at
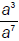 and get a4 (Why is this wrong?) OR when
and get a4 (Why is this wrong?) OR when
you look at 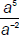 and get a3 as an answer (Why is
this wrong?)
and get a3 as an answer (Why is
this wrong?)
Simplify and express with positive exponents:
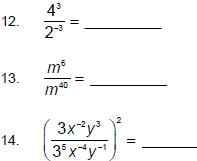
Now that we have the basic laws for exponents, apply them
to the following problems.
Express your answers with positive exponents.
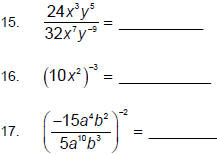
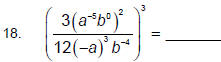
Lesson 4 Evaluating Powers
In this lesson we see exponents used in equations. Later in Math 9 you will
learn how to do a
more difficult type of equation with exponents.
Consider a problem like: 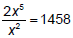
First we can reduce the fraction to ___________ = 1458
Then we can divide both sides by 2 to get __________ = _____________
Now, can we find a number to fit into the parentheses? ( )3 = 729
So, x3 = 729 and 93 = 729 . Thus, x3 = ________ and x = ____
Now try these.
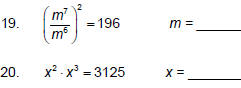
21. A number to the fourth power is squared. The result is
6561. What is the number?
Can you find another possible answer? __________ and _________
Lesson 5 Scientific Notation
Scientific notation is used to make very large and very small numbers easier to
read and to
calculate with them. The rule is that you move the decimal point as many times
as necessary
to have just one non-zero digit to the left of the decimal point and account for
the number of
times you moved the decimal by a power of 10. (It’s not as complicated as it
sounds)
Try writing the number 8,532,000 in scientific notation.
First, find the decimal point. In a whole number the decimal is assumed to be to
the right of
the one’s place digit. So, in this case it would be 8,532,000
Second, move the decimal point until it is between the 6
and the 5. How many places did it
move?
Third, write the number as the new decimal times 10 to the power of the times
you moved the
decimal. 8.532 x 10___ since we moved the decimal point 6 places.
To check: remember that 106 is 1,000,000. Then multiply 8.532 by 1,000,000 and
you get
8,532,000.
Now try writing 0.0000345 in scientific notation.
We already know where the decimal place is so we can begin with step 2.
0.0000345 becomes 3.45 and we moved the decimal _____ places to the right.
This time we write the number as 3.45 x 10____
Note that the exponent is negative since we moved the decimal to the right.
To check: remember that 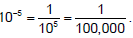 Then multiply 3.45 by
Then multiply 3.45 by 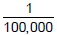 and you get
and you get
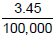 which equals 0.0000345.
which equals 0.0000345.
When you multiply or divide numbers in scientific notation, you treat the
decimal part and the
powers of 10 separately. For instance,
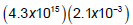
First multiply the decimals: (4.3)(2.1) = ______________
Then multiply the powers of 10: 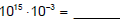
So, 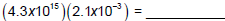
You must be careful, though, as this next example shows.
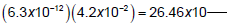 but this is NOT scientific notation! (Why?)
but this is NOT scientific notation! (Why?)
So, put this answer into scientific notation and you get ______________ x
10_____ for a final
answer. (Note: there is a problem like this on the IAD!)
Write the following in scientific notation:
22. 135,000
23. 0.00000098
Write these in standard form:
24. 3.69 x 105
25. 1.9 x 10-3
Calculate and express your answer in scientific notation:
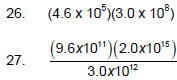 (try this without a calculator)
(try this without a calculator)


