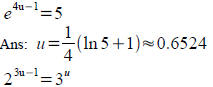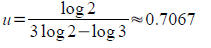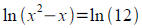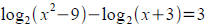1 Inverse functions
Tool: Intuitively, inverse functions help us solve equations.
For example if we have the equation x3=7 , we apply cube
root to both sides. The cube root cancels with the cube on x
so we can solve
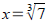
Tool: Inverse functions are defined by their
composition
properties, so g( x) is the inverse of f ( x ) iff
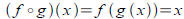 and
and
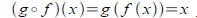 If g is the inverse of f ,
If g is the inverse of f ,
we name it f -1 (this does NOT mean
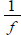 ).
).
Tool: The graphs of f and f -1 are reflections
about the
line y=x , which means if you take points on one graph,
switch the x , and y coordinates, we obtain points on the
other graph. When we switch x and y , we also exchange
domains and ranges.
NOTE: not all functions have graphs that are inverses.
Tool: A function f has an inverse that is also a function iff
a every horizontal line passes through its graph in at most one
point. (If you switch x and y , horizontal line test becomes
vertical line test for the inverse graph.
Any function passing the horizontal line test is said to be oneto-
one, i.e., every output comes from exactly one input.
Tool: Finding inverse given equation y= f ( x) . Just
switch x and y (replace one with the other where you find
them). Then solve for the new y= f -1( x ) .
NOTE: In applications we don't always use x and y . In
general we need to solve for input variable so it becomes the
new output variable, the former output becomes input.
2 Exponential functions
Tool: Exponential functions appear in the form y=bx.
The base, b must be positive. If b >1 the function is
increasing. If b <1 , the function is decreasing.
Exponential functions have horizontal asymptote y=0 .
Their domain is all real numbers and range is positive reals.
You can use the xy or ^ button on your calculator to
compute values or graph. Tool:
Transforming exponential functions.
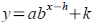
shifts the graph of bx right by h and up by k . If a is
negative, the graph flips. Tool: Exponential functions are one-to-one, i.e.,
if bx=by
, then x=y . We can use this property to solve equations.
Tool: Compound interest formula is useful for calculating
how your investments grow, or how much the credit card
companies make off of you, 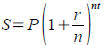 , where P is , where P is
initial amount of investment, S is amount of investment at
time t (in years). r is annual interest rate (APR) and n is
number of compounding periods (accrued interest is raked
into the pile yearly ( n=1 ), quarterly( n=4 ), monthly(
n=12 ), ...).
Tool: Continuous compounding formula. If we let n
become very large (infinite number of compounding periods)
in the compound interest formula, the whole formula reduces
to 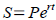 , where e=2.718281828... (there
is an ex , where e=2.718281828... (there
is an ex
button on your calculator that will approximate better than
memory).
NOTE: This same formula is used to model population
growth rates, discharge of capacitor, radioactive decay, and
lots of other stuff.
3 Properties of Logarithmic Functions
Tool: Since exponential functions y=bx are one-to-one,
we can solve for input x in terms of output y by invoking
inverse operation 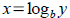 . Recall with inverse functions . Recall with inverse functions
the input and output switch places (output becomes input and
vice versa). Make sure you identify the base b and don't
confuse it with input or output.
Tool: The function
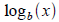 is also one-to-one and forms is also one-to-one and forms
an inverse pair with bx . So
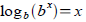 and and
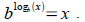
Tool: Your calculator has two log buttons
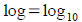 and and
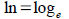 . Some logarithms you can evaluate by hand by . Some logarithms you can evaluate by hand by
writing the input as a power of the base. Tool: Common properties of logarithms may be
derived
from similar properties for exponents
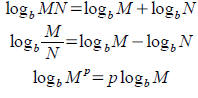
Tool: Change of base formula from base b to base c
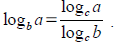 Normally this is used to convert to log Normally this is used to convert to log
keys on your calculator.
4 Graphing Logarithmic Functions
Tool: Graph of 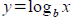 is obtained by reflecting is obtained by reflecting
y=bx about the line y=x . We can use this symmetry
and exponential graphs to generate points on log graphs.
Tool: 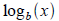 graph may be
(h , k ) shifted and reflected graph may be
(h , k ) shifted and reflected
via a 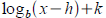
5 Exponential and Log Equations/Inequalities
Tool: Use one-to-one properties. If bx=by then x=y .
Tool: If exponential equation can't be written in terms of
powers of the same base, apply log or ln to both sides.
Tool: Quadratic equations
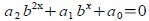 are are
solvable by substituting y=bx and factoring or applying
quadratic formula to the resulting equation. Then solve for
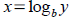 and check for extraneous solutions. and check for extraneous solutions. Tool: Use one-to-one property of logarithms.
logb x=logb y , then x=y .
Tool: Put logarithms together using the properties from
section 3 and rewrite in exponential form. |
Inverses for solving equations: Cube and
cube root are
inverse pairs. Can you think of any other inverse pairs?
What's the inverse of
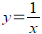 ? ?
Verifying inverses algebraically:
Verify that y=2x−2 and
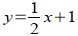 are inverses using are inverses using
the definition.
Graphs of inverses:
Can you see any relation between graphs of cube and cube
root? Can you generate one graph from the other using
symmetry?
What is inverse graph of the function
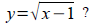 What What
are the domains and ranges?
Testing inverse graphs via horizontal line test.
What is the inverse graph of the function y=x2 + 2 ? Is it a
function?
Finding inverse functions (if possible):
Find the inverse function of f ( x )=2x−2
Find the inverse function of f ( x )=x2 + 2
Find the inverse function of f ( x )=−3( x−2)3 + 1
Application:
The equation for converting degrees Celsius to Fahrenheit is
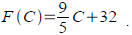 Find the inverse function C (F) for Find the inverse function C (F) for
converting from Fahrenheit to Celsius and use it to compute
what 90 F is in Celsius.
Ans: 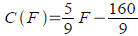 and C(90) ≈32.22 and C(90) ≈32.22
Exponential graphs.
Sketch the graphs of 3x and
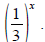 Do you notice any Do you notice any
symmetry? Why do you suppose there might be symmetry?
Sketch the transformed exponentials, indicating
asymptotes, domain and range.
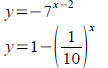
Solve for x
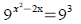
Compound interest problem:
Suppose $100,000 is invested in the bank over 5 years at 5%
compounded quarterly. What is the final return?
Ans: about $128,203.72
Suppose you have $100,000 owed on a credit card over 5
years at 25% compounded quarterly. If by some miracle you
don't have late fees, how much will you owe?
Ans: about $ 336,185.34
Continuous compounding:
Suppose $100,000 is invested in the bank over 5 years at 5%
compounded continuously. What is the final return?
Ans: about $128,402.54
Capacitor discharge:
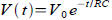 describes what happens to voltage V describes what happens to voltage V
during time t when you charge up a capacitor C with
current and then use the energy to warm up a resistor R .
For 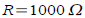 and C=0.001F and initial voltage and C=0.001F and initial voltage
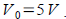 . What is the voltage after 1 second? After 5 . What is the voltage after 1 second? After 5
seconds?
Ans: 1.839 V after 1 second; 0.037 V after 5 seconds
Rearrange from exponential to logarithmic form:
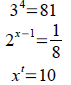
Rearrange from logarithmic to exponential form:
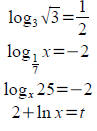
Evaluating Logarithms
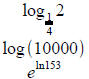
Write each expression as a sum or difference of
multiples
of logarithms:
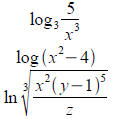
Write each expression as a single log:
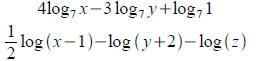
Compute:
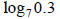
Ans: about -0.6187
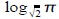
Ans: about 3.3030
Application:
Acidity is measured by pH which is given by
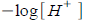
where 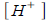 is hydrogen ion concentration moles per liter. is hydrogen ion concentration moles per liter.
How much more acidic is a substance with pH 3.2 than a
substance with pH 5.4?
Ans: about 158 times
Logarithm graphs:
Can you sketch the graph of 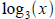 knowing the graph of knowing the graph of
3x? Evaluate points for some small values of x . What
happens to the asymptote?
Sketch the graph of
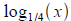 using
the graph of using
the graph of
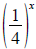 . .
Then sketch the graph
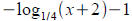 specifying specifying
domain, range, and asymptotes. Solve for t :
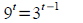 Solve for u : Solve for u :
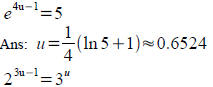
Ans:
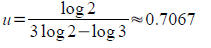
Solve for x : (a typo on p. 331 says this is not solvable
analytically. Actually it is)
9x−3x−12=0 Ans: x=log3 4≈1.2619
Solve for w :
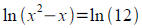
Solve for x :
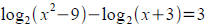
Application:
Assuming continuous compounding, how long does it double
money at 5% interest rate. At 25% interest rate?
Ans: about 13.86 years at 5%, about 2.77 years at 25%. |
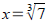
 ?
?


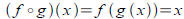 and
and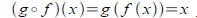 If g is the inverse of f ,
If g is the inverse of f ,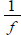 ).
).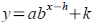
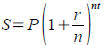 , where P is
, where P is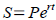 , where e=2.718281828... (there
is an ex
, where e=2.718281828... (there
is an ex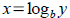 . Recall with inverse functions
. Recall with inverse functions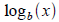 is also one-to-one and forms
is also one-to-one and forms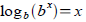 and
and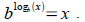
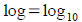 and
and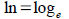 . Some logarithms you can evaluate by hand by
. Some logarithms you can evaluate by hand by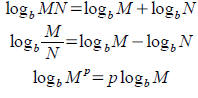
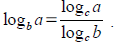 Normally this is used to convert to log
Normally this is used to convert to log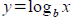 is obtained by reflecting
is obtained by reflecting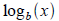 graph may be
(h , k ) shifted and reflected
graph may be
(h , k ) shifted and reflected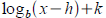
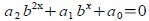 are
are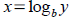 and check for extraneous solutions.
and check for extraneous solutions.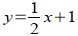 are inverses using
are inverses using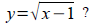 What
What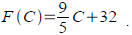 Find the inverse function C (F) for
Find the inverse function C (F) for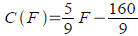 and C(90) ≈32.22
and C(90) ≈32.22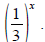 Do you notice any
Do you notice any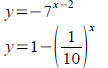
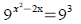
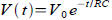 describes what happens to voltage V
describes what happens to voltage V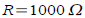 and C=0.001F and initial voltage
and C=0.001F and initial voltage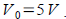 . What is the voltage after 1 second? After 5
. What is the voltage after 1 second? After 5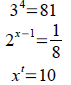
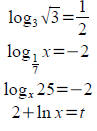
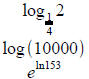
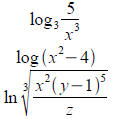
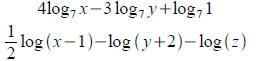
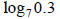
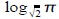
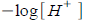
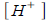 is hydrogen ion concentration moles per liter.
is hydrogen ion concentration moles per liter.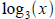 knowing the graph of
knowing the graph of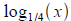 using
the graph of
using
the graph of
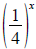 .
.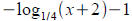 specifying
specifying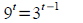 Solve for u :
Solve for u :